米田氏が企画した「競プロ典型90問」を解いていきます。
ここでは私の試行錯誤やら解説の理解やら気づきやらをメモしていこうと思います。
競プロ初心者なのでどうか温かい目で見守ってください。
なお、本記事中のPythonコードはブラウザ上で実行可能です。
よろしければ遊んでいってください。
問題
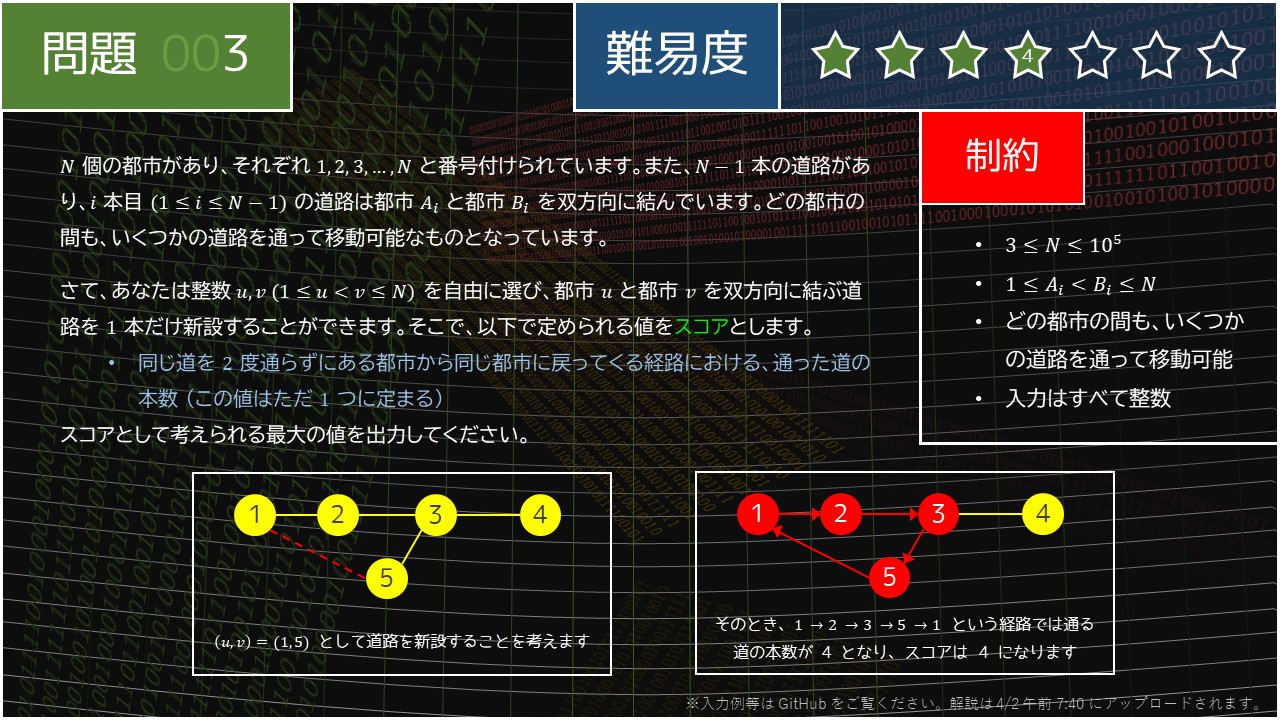kyopro_educational_90/003.jpg at main · E869120/kyopro_educational_90
003 - Longest Circular Road（★4）
やってみよう！
テストデータ・テスト関数定義 ↓
# 縮小表示
test_data = [
{'in': [3, [[1, 2], [2, 3]]], 'out': 3},
{'in': [5, [[1, 2], [2, 3], [3, 4], [3, 5]]], 'out': 4},
{'in': [10,
[[1, 2], [1, 3], [2, 4], [4, 5], [4, 6], [3, 7], [7, 8], [8, 9],
[8, 10]]],
'out': 8},
{'in': [31,
[[1, 2], [1, 3], [2, 4], [2, 5], [3, 6], [3, 7], [4, 8], [4, 9],
[5, 10], [5, 11], [6, 12], [6, 13], [7, 14], [7, 15], [8, 16], [8, 17],
[9, 18], [9, 19], [10, 20], [10, 21], [11, 22], [11, 23], [12, 24],
[12, 25], [13, 26], [13, 27], [14, 28], [14, 29], [15, 30],
[15, 31]]],
'out': 9},
{'in': [75,
[[1, 51], [3, 70], [8, 22], [6, 11], [13, 22], [14, 54], [15, 22],
[19, 52], [23, 25], [25, 26], [7, 33], [9, 35], [9, 42], [37, 56],
[40, 57], [41, 52], [28, 44], [12, 45], [12, 57], [39, 46], [39, 68],
[47, 61], [29, 48], [6, 29], [50, 65], [18, 52], [43, 54], [16, 43],
[56, 65], [38, 57], [38, 68], [24, 58], [16, 59], [10, 60], [30, 61],
[18, 62], [6, 63], [6, 30], [7, 67], [18, 68], [18, 34], [28, 69],
[28, 51], [5, 70], [5, 21], [55, 72], [22, 55], [20, 73], [36, 74],
[36, 42], [17, 42], [17, 49], [49, 66], [4, 66], [4, 10], [10, 34],
[34, 65], [30, 65], [21, 30], [20, 21], [20, 51], [27, 51], [25, 27],
[25, 31], [2, 31], [2, 53], [53, 71], [22, 71], [22, 64], [24, 64],
[7, 24], [7, 16], [16, 32], [32, 75]]],
'out': 28},
]
def test_all(f):
for i, data in enumerate(test_data):
exp = data["out"]
ans = f(*data["in"])
result = "AC" if exp == ans else "WA"
print(f"{i+1} {result}: expected: {exp}, output: {ans}")
下のmain0関数を完成させて「Run」ボタンをクリックしよう！
def main0(N, AB):
pass
test_all(main0)
自由欄
try(1st.)
考え方
- 木構造？という言葉は知っていても具体的な考え方やアルゴリズムは知らない…
- とりあえず木構造を作って、末端を2つ繋ぐ組み合わせからスコアが最大になる場合を探すか？
という感じで実装したのが以下
from itertools import combinations
def main1(N, AB):
def route(a, b, passed):
'''aからbまでに通る道の数を返す'''
passed.append(a)
if b in net[a]:
return 1
else:
for branch in net[a]:
if branch in passed:
continue
try:
return 1 + route(branch, b, passed)
except:
pass
else:
raise Exception("Here is wrong way...")
# 各都市から見て繋がっている都市のリスト
net = {i: list() for i in range(1, N+1)}
for a, b in AB:
net[a].append(b)
net[b].append(a)
# print(net)
# 末端の都市を抽出
terminals = [k for k, v in net.items() if len(v) == 1]
# 末端どうしの経路のうち最大を探す
return max([route(*pat, []) for pat in combinations(terminals, 2)]) + 1
テストデータ・テスト関数定義
test_all(main1)
結果(1st.)
あかん…
提出 #32367991 - 競プロ典型 90 問
try(2nd.)
route関数が遅いのか？と考え以下の修正
from itertools import combinations
def main2(N, AB):
dp = dict()
def route(a, b, wrongway=None):
'''aからbまでに通る道の数を返す
wrongwayからaに移動したことを示す。
'''
if (a, b, wrongway) in dp:
return dp[(a, b, wrongway)]
if b in net[a]:
ret = 1
else:
if wrongway is not None:
available = net[a].copy()
available.remove(wrongway)
else:
available = net[a]
for way in available:
ret = 1 + route(way, b, a)
if ret != 0:
break
else:
ret = -1
dp[(a, b, wrongway)] = ret
return ret
# 各都市から見て繋がっている都市のリスト
net = {i: list() for i in range(1, N+1)}
for a, b in AB:
net[a].append(b)
net[b].append(a)
# print(net)
# 末端の都市を抽出
terminals = [k for k, v in net.items() if len(v) == 1]
# 末端どうしの経路のうち最大を探す
return max([route(*pat) for pat in combinations(terminals, 2)]) + 1
test_all(main2)
結果(2nd.)
ACが2個増えた…😇
提出 #32370200 - 競プロ典型 90 問
解説
手詰まりなので解説を見てみましょう。
kyopro_educational_90/003.jpg at main · E869120/kyopro_educational_90
twitter
ふむふむ。木の直径、完全に理解した！
try(3rd.)
def main3(N, AB):
dp = dict()
def route(a, b, wrongway=None):
'''aからbまでに通る道の数を返す
wrongwayからaに移動したことを示す。
'''
if (a, b, wrongway) in dp:
return dp[(a, b, wrongway)]
if b in net[a]:
ret = 1
else:
if wrongway is not None:
available = net[a].copy()
available.remove(wrongway)
else:
available = net[a]
for way in available:
ret = 1 + route(way, b, a)
if ret != 0:
break
else:
ret = -1
dp[(a, b, wrongway)] = ret
return ret
# 各都市から見て繋がっている都市のリスト
net = {i: list() for i in range(1, N+1)}
for a, b in AB:
net[a].append(b)
net[b].append(a)
# print(net)
# 末端の都市を抽出
terminals = [k for k, v in net.items() if len(v) == 1]
# 1つの末端から、最大経路の末端を探す
one_end = None
w_routes = 0
for term in terminals[1:]:
r = route(terminals[0], term)
if r > w_routes:
w_routes = r
one_end = term
# 見つけた末端から最大経路の末端を探す
terminals.remove(one_end)
return max([route(one_end, term) for term in terminals]) + 1
test_all(main3)
結果(3rd.)
あかんやんけ！
提出 #32438989 - 競プロ典型 90 問
try(4th.)
やっぱりroute関数があかんっぽいので想定コードを見てみます。
幅優先探索(BFS)で最短距離を計算するとのこと。
あーあれね、はいはい、幅を優先する探索ね。
幅優先探索
しったかぶっても始まらないので以下参照
幅優先探索、完全に理解した
実装
from collections import deque
import operator
ig = operator.itemgetter
def main4(N, AB):
def bfs(start):
'''startから最短距離が最大の都市と距離を返す'''
q = deque([start])
passed = {start: 0}
while len(q):
n = q.popleft()
for dest in tree[n]:
if not dest in passed:
q.append(dest)
passed[dest] = passed[n] + 1
return max(passed.items(), key=ig(1))
tree = {i:list() for i in range(1, N+1)}
for a, b in AB:
tree[a].append(b)
tree[b].append(a)
end1, _ = bfs(1)
_, ans = bfs(end1)
return ans + 1
test_all(main4)
結果(4th.)
無事ACとなりました。
提出 #32455958 - 競プロ典型 90 問
まとめ
- 2回目の
route関数でメモ化を行ったが、引数がroute(出発点、目的点)というかたちのため「一つの出発点から複数の目的点の最短経路を列挙する」というケースには適さなかった？
- でも「複数の出発点から一つの目的点までの最短経路を列挙する」にしても、目的点からの最短経路を幅優先探索すればいいだけだし、結局コーディングのレベルとアルゴリズムの知識が不足してるってことか…
地道に勉強して武器を増やしていこうと思います。
自由欄
